This post gives a brief introduction to the basic structure of LSTM (Long-Short Term Memory) model with an intuitive figures and explanations. Let's interpret "gate" as "rate" or "weight" for grasping the concept of LSTM faster since we are not engineers but finance-related practitioners.

Understanding the LSTM model

I will explain the LSTM model and then talk about the RNN model by eliminating the LSTM gates one by one. Now let's understand the structure of LSTM model.

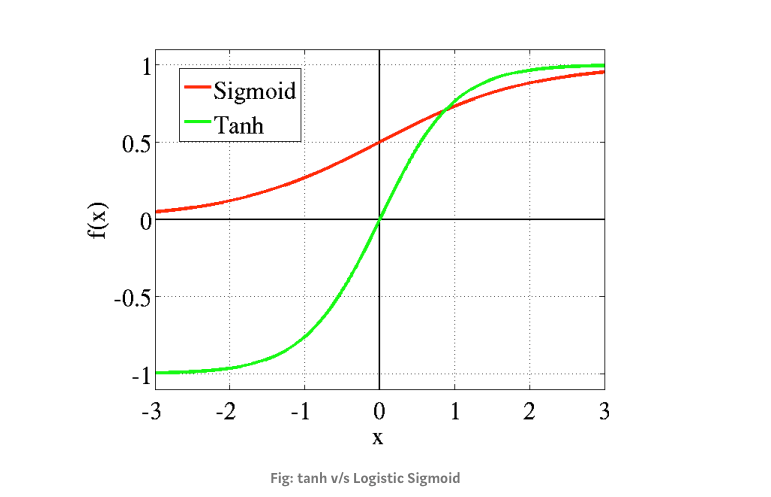
Activation function : Sigmoid versus Tanh

LSTM uses two types of activation functions: sigmoid (S) and hyperbolic tangent or tanh (T). The sigmoid determines the ratio or rate of information and tanh normalizes information into the range between -1 and 1. These two activation function have the following responses respectively.

\[\begin{align} sigm(x) = \frac{1}{1+e^{-x}}, \quad tanh(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \end{align}\]

Input, Output (State) and Memory

LSTM is a function so that it has input (\(x_{t-1}\), \(h_{t-1}\)) and output (\(h_t\)). It is a variant of RNN model and has two temporal dependence mechanism: short-term memory (\(h_t\)) and long-term memory (\(C_t\)).

These variables are summarized as follows.

• \(C_{t}\) : memory cell
• \(h_{t-1}\) : previous output or state
• \(x_t\) : input data or input sequence at time t (i.e. \(y_{t-1}\))
• \(h_t\) : hidden state or output (fitted y value)
• \(y_t\) : target data

The inner structure of LSTM

Given \(x_t\) (current input) and \(h_{t-1}\) (previous state or output), the inner structure of LSTM is defined by a set of equations as follows.

The main component of LSTM is the memory cell (\(C_t\)) which penetrates through the whole layers. This is adjusted and added and finally reduced into output combined with the current and previous information.

At time \(t\),

• \(C_{t-1}\) enters into the LSTM layer and some portion of it is deleted by \(f_t\), which is the forget rate.
• The current memory cell (\(\tilde{C}_t\)) is constructed by the current and previous short-term information (\(x_t, h_{t-1}\)) and also some portion of it is selected by \(i_t\), which is the input rate.
• The updated memory cell (\(C_t\)) is determined by the sum of 1) and 2). This is essentially a weighted average like an updating of th Kalman filter and is transferred into the next LSTM layer.
• As \(C_t\) contains information of the previous state, current input, and the memory cell, it determines the current output (\(h_t\)) which is some portion of the updated memory cell (\(C_t\)) by adjusting the output rate (\(o_t\)).

I use the word "rate" rather than "gate" since I think that "rate" has a bound between 0 and 1 (ratio or weight) and reflects the functionalities of three gates more intuitively.

These set of equations for the LSTM model can be illustrated by the following figure.

It is worth to note that the current information (\(x_t\)) and the previous state (\(h_{t-1}\)) are fed into the LSTM layer and convey short-term information and the memory cell governs the relatively long-term information.

RNN (Recurrent Neutral Network)

If the memory cell is absent, \(C_{t-1}\), \(C_{t}\) and \(f_t\) can be deleted. This also leads to \(i_t\) being one (full weight) since \(\tilde{C}_t\) is not calculated. This reasoning leads to the following simple RNN equation.
\[\begin{align} h_t = tanh(W x_t + U h_{t-1} + b) \end{align}\]

Concluding Remarks

This post gives short introduction to the basic structure of LSTM model with an intuitive figures and explanations. The remaining job is to know how to implement LSTM or RNN model using Keras or Tensorflow. \(\blacksquare\)