Excel Solver using VBA macro : Nelson-Siegel yield curve fitting

This post shows how to run an Excel solver using VBA macro. If the number of optimization problems are more than two, every time we switch among these optimization problems, we have to change each settings for solver. It is tedious and may cause key-input errors. In this case, this approach is useful.

Excel Solver using VBA macro

Nelson-Siegel Yield Curve Fitting

We use Excel solver to get a solution of non-linear least squares problem. I take my favorite model, Nelson-Siegel model, as an example,

As can be seen in the above figure, a term structure of yields is fitted with initial guesses for parameters. we need to estimate these 4 Nelson-Siegel parameters (b0, b1, b2, lambda).

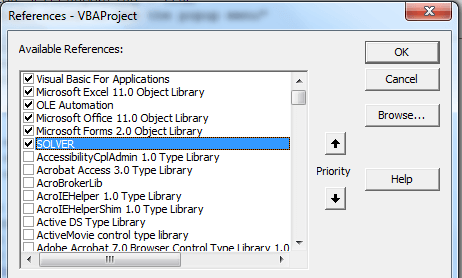
VBA editor ➔ Tools ➔ References ➔ Solver

To use Solver in VBA macro, Go to Tools ➔ Reference in Visual Basic Editor menu. From the references list, choose “Solver” and click on Ok to use it.

Some Excel Formula

There are three block of Excel formula : RMSE (B4), b0+b1 (G4), fitted yields (D7~D20).

RMSE (B4) is a square root of mean of fitting errors. Curly braces denotes CTRL+SHIFT+ENTER as you already know.

cell B4 ⇒ {=SQRT(AVERAGE((C7:C20-D7:D20)^2))}

b0+b1 (G4) is sum of b0 and b1, which means a short-term rate is not negative although this is not the case for some European country. It depends on which country's yield curve is used.

cell G4 ⇒ = C4+D4

Nelson-Siegel fitted yields (D7~D20) have its excel formula as follows.

cell D7 ⇒ = C4+D4*(1-EXP(-F4*B7))/(F4*B7)+E4*((1-EXP(-F4*B7))/(F4*B7)-EXP(-F4*B7)) ... cell D20 ⇒ = C4+D4*(1-EXP(-F4*B20))/(F4*B20)+E4*((1-EXP(-F4*B20))/(F4*B20)-EXP(-F4*B20))

Objective, Parameters, Constraints

In this Nelson-Siegel fitting problem, an objective function is RMSE and parameters are b0, b1, b2 and lambda with some constraints : b0 > 0, b0+b1>0, 0.01 &lt lambda &lt 0.1.

range	description
B4	objective function value
C4:F4	parameters to be found
G4	combined constraints

Some Arguments for Solver

As it is boring to enumerate a list of arguments of functions, I'll present only some necessary part of it.

SolverOk(SetCell, MaxMinVal, ValueOf, ByChange, Engine, EngineDesc)

MaxMinVal	value
1	Maximize
2	Minimize
3	Matched to a "ValueOf"

SolverAdd(CellRef, Relation, FormulaText)

Relation	value
1	less than (<=)
2	equal to (=)
3	greater than (>=)
4	integers
5	either 0 (zero) or 1
6	all different and integers

Excel VBA macro code

Excel VBA code below implements the above explanations so that you can easily grasp out. This macro function is linked to a button you place it on the spreadsheet.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

Sub run_solver_ns()       ' clear and start     SolverReset              ' uncheck Non-negative option     SolverOptions AssumeNonNeg:=False          ' objective and parameters     SolverOk SetCell:="$B$4", MaxMinVal:=2, ValueOf:="0", _              ByChange:="$C$4:$F$4"                   ' b0 >=0     SolverAdd CellRef:="$C$4", Relation:=3, FormulaText:="0.000000001"          ' b0+b1 >=0     SolverAdd CellRef:="$G$4", Relation:=3, FormulaText:="0.000000001"          ' 0.01 < lambda < 0.1     SolverAdd CellRef:="$F$4", Relation:=3, FormulaText:="0.01"     SolverAdd CellRef:="$F$4", Relation:=1, FormulaText:="0.1"          ' run     SolverSolve True          End Sub   Colored by Color Scripter

cs

Running this macro by clicking button estimates parameters of Nelson-Siegel model and generate fitted yield curve as follows.

Concluding Remarks

In this post we use VBA macro to run the Excel solver. Next time, it will be extended to multiple runs of Excel solver for time series data. \(\blacksquare\)