Run Excel Solver multiple times : Period-by-Period Estimations of Nelson-Siegel model

This post shows how to run an Excel solver using VBA macro multiple times. As an example, we take period by period estimations of Nelson-Siegel model.

Run Excel Solver multiple times using VBA macro

Sequential Nelson-Siegel Yield Curve Fittings

We use Excel solver to get solutions of non-linear least squares problems. I take also Nelson-Siegel model as an example. The following spreadsheet contains monthly yield curves (left block) so that we try to estimate monthly Nelson-Siegel parameters (middle block) and get fitted yield curves (right block).

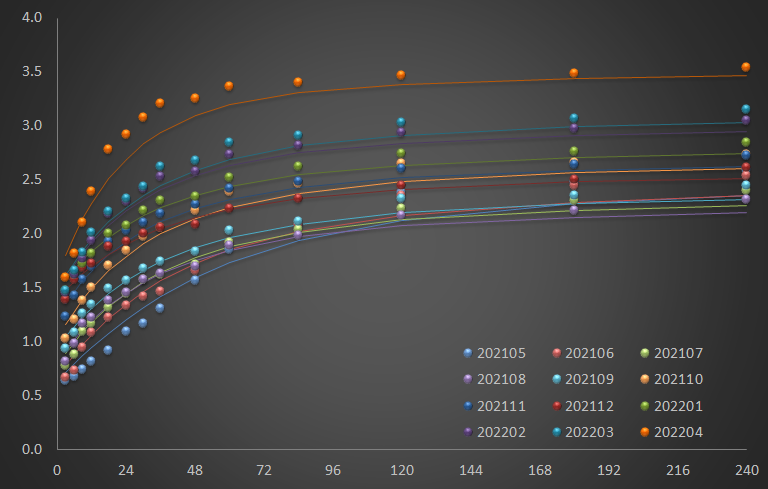
As can be seen in the figure below, monthly term structure of yields are fitted with initial guesses for parameters. we need to estimate these 4 Nelson-Siegel parameters (b0, b1, b2, lambda) period by period.

Some Excel Formula

There are three block of Excel formula like the previous post: RMSE (column P), b0+b1 (column U), fitted yields (column from V to AI). For instance, I present their Excel formula for the first row.

RMSE (column P) are a set of square root of mean of fitting errors. Curly braces denotes CTRL+SHIFT+ENTER as you already know.

cell P4 ⇒ {=SQRT(AVERAGE((B4:O4-V4:AI4)^2))}

b0+b1 (column U) are sums of b0 and b1, which means a short-term rate is not negative although this is not the case for some European country. It depends on which country's yield curve is used.

cell U4 ⇒ =Q4+R4

Nelson-Siegel fitted yields (column from V to AI) have their excel formula as follows.

cell V4 ⇒ =Q4+R4*(1-EXP(-T4*V3))/(T4*V3)+S4*((1-EXP(-T4*V3))/(T4*V3)-EXP(-T4*V3)) ... cell AI4 ⇒ =Q4+R4*(1-EXP(-T4*AI3))/(T4*AI3)+S4*((1-EXP(-T4*AI3))/(T4*AI3)-EXP(-T4*AI3))

Objective, Parameters, Constraints

In this Nelson-Siegel fitting problem, an objective function is RMSE and parameters are b0, b1, b2 and lambda with some constraints : b0 > 0, b0+b1>0, 0.01 &lt lambda &lt 0.1. For instance, I present their Excel formula for the first row.

range	description
P4	objective function value
Q4:T4	parameters to be found
U4	combined constraints

Excel VBA macro code

Excel VBA code below implements the above explanations. This macro function is linked to a button you place it on the spreadsheet. As can be seen in the code below, core optimization block is the same as the previous post except for-loop iteration for monthly calculations.

In particular, (long) integer sr(=3+i) is used to indicate a proper row number to access the corresponding yield data, RMSE, parameters, restriction, and fitted yield curve.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

Sub run_solver_ns_multiple()       Dim i As Long, sr As Long          For i = 1 To 12              sr = 3 + i              ' clear and start         SolverReset                      ' uncheck Non-negative option         SolverOptions AssumeNonNeg:=False                  ' objective and parameters         SolverOk SetCell:="$P$" & sr, MaxMinVal:=2, ValueOf:="0", _                  ByChange:="$Q$" & sr & ":$T$" & sr                           ' b0 >=0         SolverAdd CellRef:="$Q$" & sr, Relation:=3, FormulaText:="0.000000001"                  ' b0+b1 >=0         SolverAdd CellRef:="$U$" & sr, Relation:=3, FormulaText:="0.000000001"                  ' 0.01 < lambda < 0.1         SolverAdd CellRef:="$T$" & sr, Relation:=3, FormulaText:="0.01"         SolverAdd CellRef:="$T$" & sr, Relation:=1, FormulaText:="0.1"                  ' run         SolverSolve True              Next i      End Sub   Colored by Color Scripter

cs

Running this macro by clicking button estimates monthly parameters of Nelson-Siegel model period by period and generate fitted yield curves as follows.

Concluding Remarks

In this post we use VBA macro to run the Excel solver multiple times. This will be useful for some repeated optimization works such as daily, weekly, or monthly yield curve estimations and so on. \(\blacksquare\)